斐波拉契数列
1,1,2,3,5,8,13...,状态转移方程:
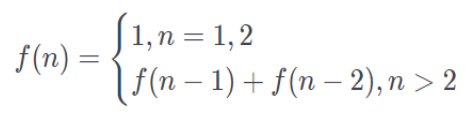
暴力递归
def main(a):
if a == 1 or a == 2:
return 1
return main(a-1) + main(a-2)时间复杂度为O(2^n),有如下递归树:
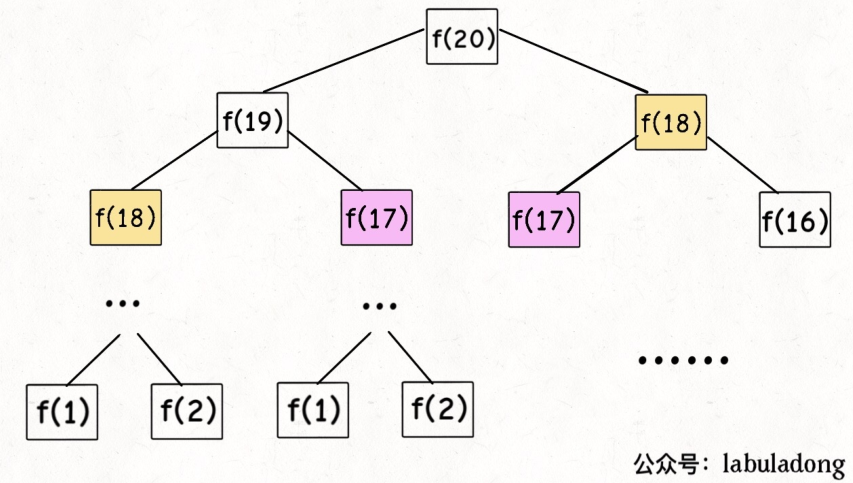
我们可以看到许多的计算都重复了,例如下面的f(18)等,那么如何避免这个问题呢?有效的方法就是将第一次计算出的f(18)的结果保留下来,如果下次再计算到这个f(18)的时候直接将结果取出来即可,简称备忘录方法,如下:
带备忘录的递归解法
memo = dict()
def main(a):
if a == 1 or a == 2:
return 1
if a in memo:
return memo[a]
memo[a] = main(a-1) + main(a-2)
return main(a-1) + main(a-2)DP table解法
自底向上优化
dp = []
def main(a):
if a == 1 or a == 2:
return 1
dp.append(1)
dp.append(1)
for i in range(2, a):
dp.append(dp[i - 1] + dp[i - 2])
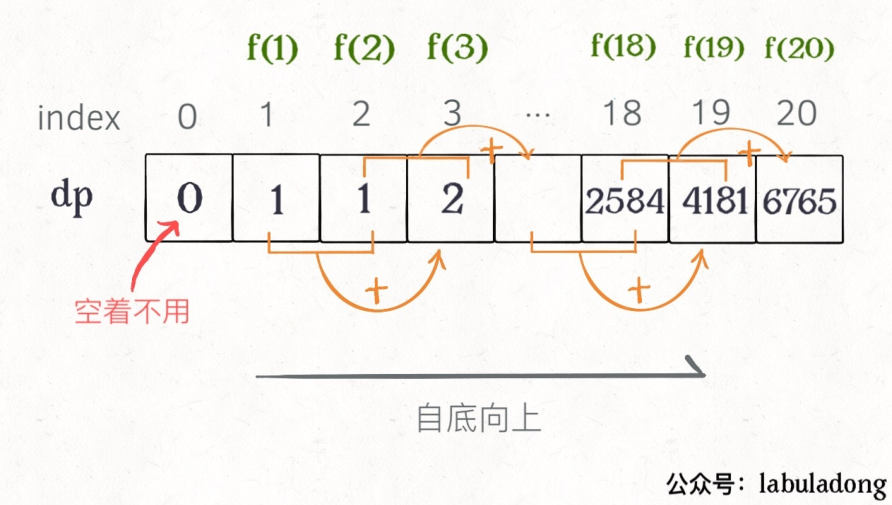
return dp[a-1]原理图如下(emmmmm,图是搬运过来的,所以前面的第0位还是用到了的,往前移一位就行了)
优化
再进行空间复杂度的优化
def main(a):
if a == 1 or a == 2:
return 1
prev = 1
curr = 1
for i in range(3, a + 1):
num = prev + curr
prev = curr
curr = num
return curr由原来的时间复杂度O(2^n)变为了O(n),空间复杂度降为O(1)
凑零钱问题
假设给你k中面值的硬币,面值分别为c1,c2,c3 ... ck,每种硬币的数量无限,再给一个总金额amount,问最少需要几枚硬币凑出这个金额,如果不可能凑出,则返回-1
状态转移方程:
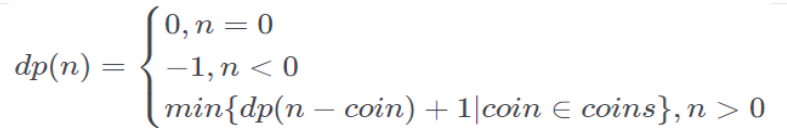
暴力递归
def coinChange(coins, amount):
def main(n):
if n == 0: # 当n - coin = 0 的时候说明这条路走的通
return 0
if n < 0: # 当n - coin < 0 的时候则说明这条路走不通
return -1
res = float("INF") # float("INF")为正无穷大,负无穷大则为float("-INF")
for coin in coins: # 递归列表
sub = main(n - coin) # 取出一个值n就要减去那个值
if sub == -1:
continue # 当main函数的返回值为-1的时候,这条路走不通,则挑出循环
res = min(res, 1 + sub) # 当到了树的最低下,上面的if语句没有执行跳出去,则使res=sub+1
return res if res != float("INF") else -1 # 这条路走的通,则返回res的值给sub,结合上面的一条语句进行计数
return main(amount)
# 最后取出第一个选择的那个数字的时候计算出的res最小值,然后再把每个数字的最小值拿出来比较得出最终的最小值
if __name__ == "__main__":
print(coinChange([1, 2, 5], 11))以上的路走的通的意思是能够凑出这些硬币,递归图如下:
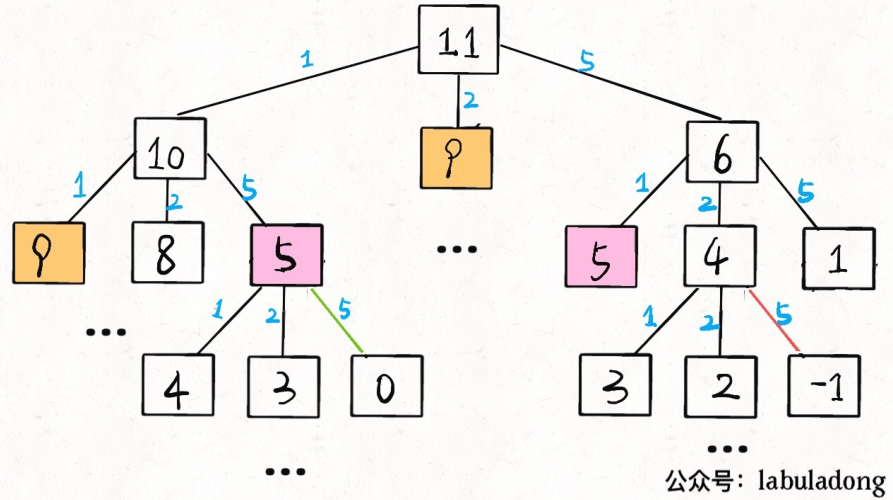
带备忘录的递归解法
def coinChange(coins, amount):
memo = dict()
def main(n):
if n in memo: # 查找备忘录,避免重复计算,就是计算以上颜色相同的部分
return memo[n]
if n == 0:
return 0
if n < 0:
return -1
res = float("INF")
for coin in coins:
sub = main(n - coin)
if sub == -1:
continue
res = min(res, 1 + sub)
memo[n] = (res if res != float("INF") else -1)
return memo[n]
return main(amount)
if __name__ == "__main__":
print(coinChange([1, 2, 5], 11))DP table解法
def main(coins, a):
for i in range(a + 1):
dp.append(i)
for i in range(a + 1):
for coin in coins:
if i - coin < 0:
continue
dp[i] = min(dp[i], 1 + dp[i - coin])
return -1 if dp[a] == (a + 1) else dp[a]
if __name__ == "__main__":
dp = []
print(main([1, 2, 5], 11))演示图如下:
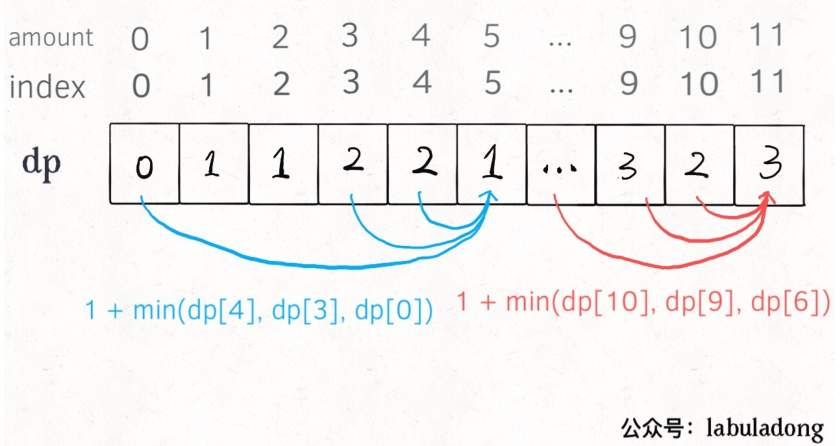
借用大佬的一句话:
计算机解决问题其实没有任何奇技淫巧,他唯一的解决方法就是穷举,穷举所有的可能性。算法设计无非就是先思考“如何穷举”,然后再追求“如何聪明的穷举”
最长递增子序列

动态规划解法
动态规划的核⼼设计思想是数学归纳法。
假设当结论在k<n的时候成立,然后想办法证明k=n的时候结论也成立,如果能够证明的出来,那么就说明这个结论对于任何数都成立,再看到这个题目,假如我们能够证明,最后一个nums[i]的值大于前一个nums[j]的值,那么就能够证明出他和nums[j]所构成的最长递增子序列能够结合,随后再将长度加一,且将nums[i]加入到这个最长递增子序列中,即:
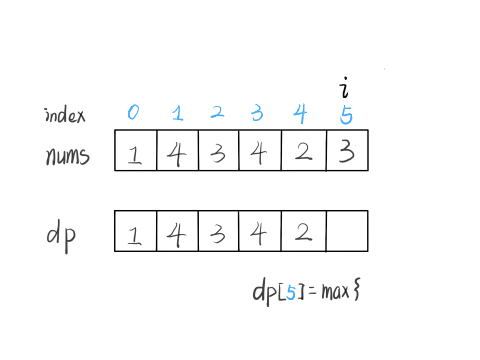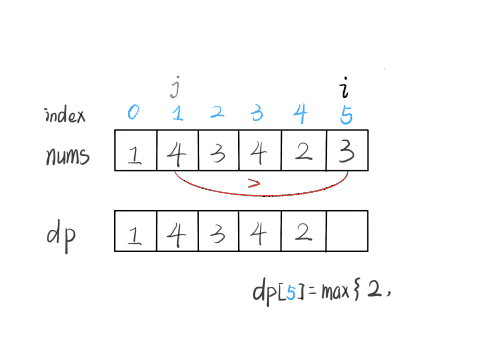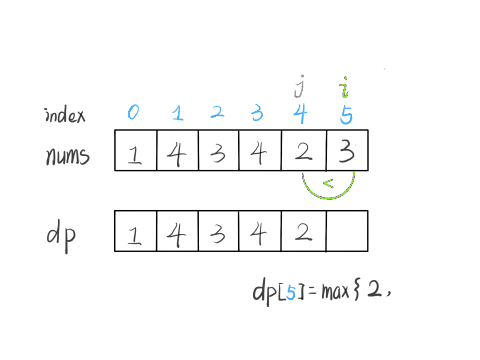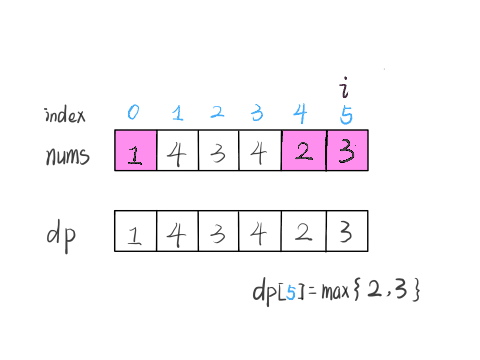
代码实现
def main(nums):
res = 0
dp = [] # 定义每一位数的最长递增子序列
for i in range(len(nums)):
dp.append(1) # 令每一位的初始值为1
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1) # dp[i]表示nums[i]这个数结尾的最长递增子序列的长度
for i in range(len(dp)):
res = max(res, dp[i])
return res
if __name__ == "__main__":
print(main([8, 7, 10]))可见时间复杂度为O(n^2)
二分查找解法
将输入的序列分成若干堆,需要遵循以下规则:
只能把小的数字压到比它大的数字上,也就是用小的数字覆盖掉原来大的,那么如何去压呢?那么就看该数字该如何选择了,如果当前数字较大没有可以放置的堆,那么就在边上新建一个堆,再把数字放进去,如果有多个堆可以选择,则选择这多个堆中考最左边的位置,保证堆顶的数字是有序的了,就像这样(A是最大的)
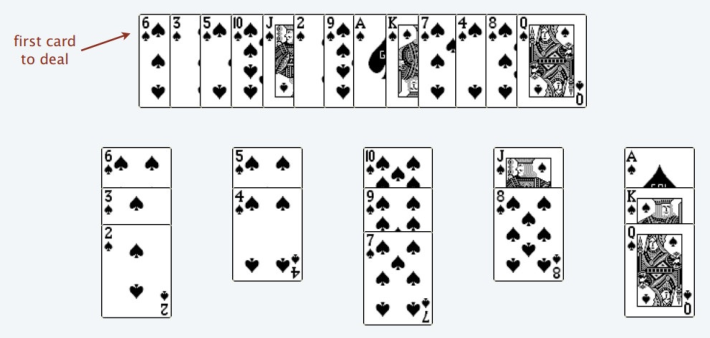
这样堆顶的数字就可以形成一个最长递增子序列,当然序列肯定不止一个,如下:
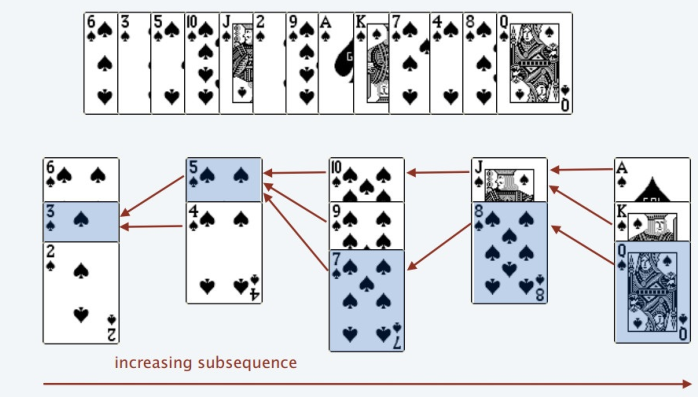
能够保证得出最长递增子序列,随后在查找该放在哪个堆的时候使用二分法查找就可以提高效率,代码如下:
def main(nums):
piles = 0 #定义最长递增子序列的长度
top = [] # 定义每一位数的最长递增子序列
for i in range(len(nums)):
top.append(0) # 令每一位的初始值为1
for i in range(len(nums)):
poker = nums[i]
left = 0
right = piles
while left < right:
mid = int((left + right) / 2)
if top[mid] > poker:
right = mid
elif top[mid] < poker:
left = mid + 1
else:
right = mid
if left == piles:
piles += 1 # 最长递增子序列的长度加一
top[left] = poker
return piles
if __name__ == "__main__":
print(main([8, 7, 6, 1, 4, 10]))编辑距离
先来看一下题目描述

递归解法
def minDistance(s1, s2):
def dp(i, j):
if i == -1:
return j + 1 # 假如当s1字符串循环i次循环完了,j还有剩下的部分就直接全部进行一个操作j+1次即可,因为还剩下j+1个字符
if j == -1:
return i + 1 # 同上
if s1[i] == s2[j]:
return dp(i - 1, j - 1) # 若相等直接跳过进行下一个字符的判断
else:
return min(dp(i, j - 1) + 1, # 插入
dp(i - 1, j - 1) + 1, # 替换
dp(i - 1, j) + 1) # 删除
return dp(len(s1) - 1, len(s2) - 1)
if __name__ == "__main__":
print(minDistance("apple", "add"))以上是将apple和add两个字符串进行转换,得出的结果为4,即所需操作的最小值
带备忘录的递归解法
def minDistance(s1, s2):
memo = dict() # 备忘录
def dp(i, j):
if (i, j) in memo:
return memo[(i, j)]
if i == -1:
return j + 1 # 假如当s1字符串循环i次循环完了,j还有剩下的部分就直接全部进行一个操作j+1次即可,因为还剩下j+1个字符
if j == -1:
return i + 1 # 同上
if s1[i] == s2[j]:
memo[(i, j)] = dp(i - 1, j - 1) # 若相等直接跳过进行下一个字符的判断
else:
memo[(i, j)] = min(dp(i, j - 1) + 1, # 插入
dp(i - 1, j - 1) + 1, # 替换
dp(i - 1, j) + 1) # 删除
return memo[(i, j)]
return dp(len(s1) - 1, len(s2) - 1)
if __name__ == "__main__":
print(minDistance("apple", "add"))DP table解法
自底向上
首先确定dp数组的含义,dp数组是一个二维数组,如下:
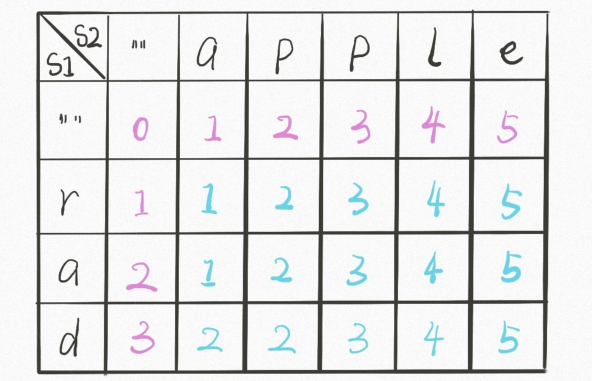
dp[i][j]存储着s1[i]和s2[j]的最小编辑距离,各相邻的数据之间有如下关系:
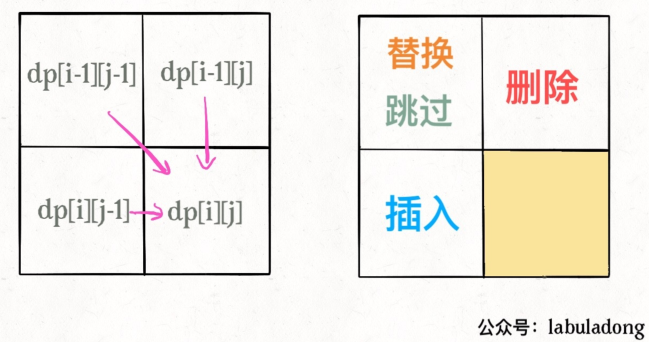
于是就可以写出以下代码:
def minDistance(s1, s2):
m = len(s1)
n = len(s2)
dp = dict()
dp[(0, 0)] = 0
for i in range(1, m + 1):
dp[(i, 0)] = i
for i in range(1, n + 1):
dp[(0, i)] = i
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i - 1] == s2[j - 1]:
dp[(i, j)] = dp[(i - 1, j - 1)]
else:
dp[(i, j)] = min(dp[(i, j - 1)] + 1,
dp[(i - 1, j - 1)] + 1,
dp[(i - 1, j)] + 1)
return dp[(m, n)]
if __name__ == "__main__":
print(minDistance("apple", "add"))随后还可以将步骤推出来:
def minDistance(s1, s2):
m = len(s1)
n = len(s2)
dp = dict()
a = dict() # 记录每一步的操作 0:啥都不做,1:插入,2:替换,3:删除
dp[(0, 0)] = 0
a[(0, 0)] = 0
for i in range(1, m + 1):
dp[(i, 0)] = i
a[(i, 0)] = 3
for i in range(1, n + 1):
dp[(0, i)] = i
a[(0, i)] = 1
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i - 1] == s2[j - 1]:
dp[(i, j)] = dp[(i - 1, j - 1)] # 不动,也就是相同直接跳过 0
a[(i, j)] = 0
else:
dp[(i, j)] = min(dp[(i, j - 1)] + 1, # 插入 1
dp[(i - 1, j - 1)] + 1, # 替换 2
dp[(i - 1, j)] + 1) # 删除 3
if dp[(i, j)] == dp[(i, j - 1)] + 1:
a[(i, j)] = 1
elif dp[(i, j)] == dp[(i - 1, j - 1)] + 1:
a[(i, j)] = 2
elif dp[(i, j)] == dp[(i - 1, j)] + 1:
a[(i, j)] = 3
for i in range(n + 1):
for j in range(m + 1):
print(a[(j, i)], end="")
print()
return dp[(m, n)]
if __name__ == "__main__":
print(minDistance("apple", "add"))以上代码将输出:
033333
103333
112222
111222
4从后面往前推就行,0,2代表对角(跳过/替换),1代表向上(插入),3代表向左(删除)
寻找到0的最佳捷径就OK
高楼扔鸡蛋
题目:
目前有一栋1到N共N层的楼,然后给你K鸡蛋(K至少为1),现在确定这栋楼存在楼层0<=F<=N,在这层楼将鸡蛋扔下去鸡蛋恰好没有碎(高于F的楼层都会碎,低于F的楼层都不会碎),现在问,最坏的情况下,你至少要扔多少次鸡蛋,才能确定这个楼层F?
带备忘录的递归解法
def main(K, N): # K个鸡蛋,N层楼
memo = dict()
if K == 0:
return N
if N == 0:
return 0
if (K, N) in memo:
return memo[(K, N)]
res = float("INF")
for i in range(1, N + 1):
res = min(res, max(main(K - 1, i - 1), main(K, N - i)) + 1) # 在max最坏的情况下,求min最优解,main(K - 1, i - 1)表示碎了,main(K, N - i)表示没碎
memo[(K, N)] = res
return res
if __name__ == "__main__":
print(main(1, 100))二分法优化
def main(K, N): # K个鸡蛋,N层楼
memo = dict()
if K == 0:
return N
if N == 0:
return 0
if (K, N) in memo:
return memo[(K, N)]
res = float("INF")
lo = 1
hi = N
while lo <= hi:
mid = (lo + hi) // 2
broken = main(K - 1, mid - 1) # 碎
not_broken = main(K, N - mid) # 没碎
# res = min(max(碎, 没碎) + 1)
if broken > not_broken:
hi = mid - 1
res = min(res, broken + 1)
else:
lo = mid + 1
res = min(res, not_broken + 1)
memo[(K, N)] = res
return res
if __name__ == "__main__":
print(main(1, 100))未完待续。。。



若没有本文 Issue,您可以使用 Comment 模版新建。
GitHub Issues